接上一篇迷宫问题01讲,之前一篇只解决了能不能走出去,而并没有知道怎么走。最短的路线是怎样的,这一篇就解决了这些问题。
题目还是看上一篇。代码:
1 | import java.util.Scanner; |
输出情况:
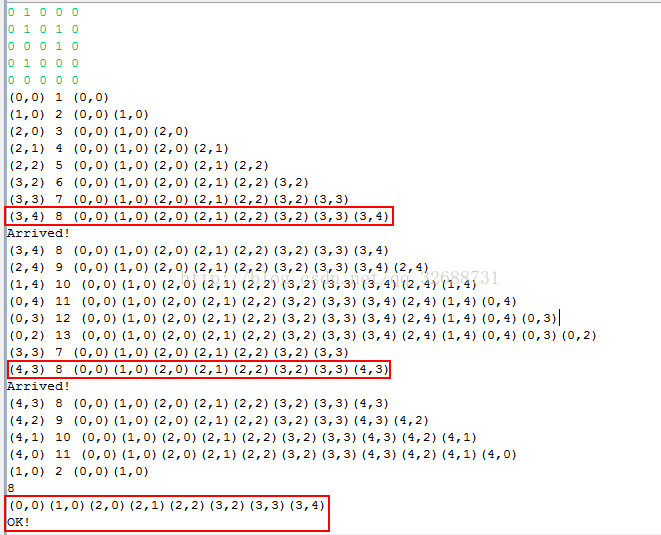
有个问题就是同样都是最短路径,怎么选择那一条走??
接上一篇迷宫问题01讲,之前一篇只解决了能不能走出去,而并没有知道怎么走。最短的路线是怎样的,这一篇就解决了这些问题。
题目还是看上一篇。代码:
1 | import java.util.Scanner; |
输出情况:

有个问题就是同样都是最短路径,怎么选择那一条走??
算法训练 开心的金明
时间限制:1.0s 内存限制:256.0MB
问题描述
金明今天很开心,家里购置的新房就要领钥匙了,新房里有一间他自己专用的很宽敞的房间。更让他高兴的是,妈妈昨天对他说:“你的房间需要购买哪些物品,怎 么布置,你说了算,只要不超过N元钱就行”。今天一早金明就开始做预算,但是他想买的东西太多了,肯定会超过妈妈限定的N元。于是,他把每件物品规定了一 个重要度,分为5等:用整数1~5表示,第5等最重要。他还从因特网上查到了每件物品的价格(都是整数元)。他希望在不超过N元(可以等于N元)的前提 下,使每件物品的价格与重要度的乘积的总和最大。
设第j件物品的价格为v[j],重要度为w[j],共选中了k件物品,编号依次为 j1,j2,……,jk,则所求的总和为:
v[j1]w[j1]+v[j2]w[j2]+ …+v[jk]w[jk]。(其中为乘号)
请 你帮助金明设计一个满足要求的购物单。
输入格式
输入文件 的第1行,为两个正整数,用一个空格隔开:
N m
(其中N(<30000)表示总钱 数,m(<25)为希望购买物品的个数。)
从第2行到第m+1行,第j行给出了编号为j-1的物品的基本数据,每行有2个非负整数
v p
(其中v表示该物品的价格(v<=10000),p表示该物品的重要度(1~5))
输出格式
输出文件只有一个正整数,为不超过总钱数的物品的价格与重要度乘积的总和的最大值(<100000000)。
样例输入
1000 5
800 2
400 5
300 5
400 3
200 2
样例输出
3900
数据规模和约定
这个题差点做不出来的,还是看以前的代码才勉强做出来了
代码:
1 | import java.util.Scanner; |
算法训练 Hankson的趣味题
时间限制:1.0s 内存限制:64.0MB
锦囊1
枚举或数论方法。
锦囊2
x是a1的倍数,b1的约数,可以枚举b1所有的约数来判断是否满足条件。 也可以使用数论的方法,将a0, a1, b0, b1分解因数,可以找到x对于每个质因子的范围,根据这个可以得到答案的公式(将每个质因子的范围相乘)。
问题描述
Hanks 博士是BT (Bio-Tech,生物技术) 领域的知名专家,他的儿子名叫Hankson。现 在,刚刚放学回家的Hankson 正在思考一个有趣的问题。 今天在课堂上,老师讲解了如何求两个正整数c1 和c2 的最大公约数和最小公倍数。现 在Hankson 认为自己已经熟练地掌握了这些知识,他开始思考一个“求公约数”和“求公 倍数”之类问题的“逆问题”,这个问题是这样的:已知正整数a0,a1,b0,b1,设某未知正整 数x 满足: 1. x 和a0 的最大公约数是a1; 2. x 和b0 的最小公倍数是b1。 Hankson 的“逆问题”就是求出满足条件的正整数x。但稍加思索之后,他发现这样的 x 并不唯一,甚至可能不存在。因此他转而开始考虑如何求解满足条件的x 的个数。请你帮 助他编程求解这个问题。
输入格式
输入第一行为一个正整数n,表示有n 组输入数据。
接下来的n 行每 行一组输入数据,为四个正整数a0,a1,b0,b1,每两个整数之间用一个空格隔开。输入 数据保证a0 能被a1 整除,b1 能被b0 整除。
输出格式
输出共n 行。每组输入数据的输出结果占一行,为一个整数。
对于每组数据:若不存在这样的 x,请输出0; 若存在这样的 x,请输出满足条件的x 的个数;
样例输入
2
41 1 96 288
95 1 37 1776
样例输出
6
2
样例说明
第一组输入数据,x 可以是9、18、36、72、144、288,共有6 个。
第二组输入数据,x 可以是48、1776,共有2 个。
数据规模和约定
对于 50%的数据,保证有1≤a0,a1,b0,b1≤10000 且n≤100。
对于 100%的数据,保证有1≤a0,a1,b0,b1≤2,000,000,000 且n≤2000。
常规的穷举法,超时了。只过了50%的数据。没学过高等数学,不明白提示的意思|
代码:
1 | import java.util.Scanner; |