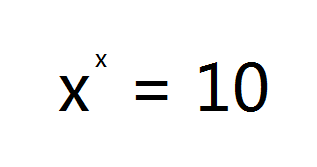1、则表达式 java中提供了对正则表达式的支持。
如下代码用来检验一个四则运算式中数据项的数目,请填写划线部分缺少的代码。
注意:只填写缺少代码,不要写任何多余内容,例如,已有的双引号。
代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 package 校内选拔2015; public class T1 { public static int f(String s) { return s.split("\\p{Punct}").length; } public static void main(String[] args) { System.out.println(f("12+35*5-2*18/9-3")); //7 System.out.println(f("354*12+3-14/7*6")); //6 } }
2、达到或超过 15.0 1/1 + 1/2 + 1/3 + 1/4 + … 在数学上称为调和级数。
它是发散的,也就是说,只要加上足够多的项,就可以得到任意大的数字。
但是,它发散的很慢:
前1项和达到 1.0
那么,请你计算一下,要加多少项,才能使得和达到或超过 15.0 呢?
请填写这个整数。
注意:只需要填写一个整数,不要填写任何多余的内容。比如说明文字。
代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 package 校内选拔2015; import java.math.BigDecimal;; public class T2 { public static void main(String[] args) { //1/1 + 1/2 + 1/3 + 1/4 + ... 在数学上称为调和级数。 BigDecimal bd=BigDecimal.ONE; BigDecimal sum=BigDecimal.ZERO; int i=1;//1835422 while(sum.subtract(BigDecimal.valueOf(15)).doubleValue()<0) { sum=sum.add(bd.divide(BigDecimal.valueOf(i),120,BigDecimal.ROUND_HALF_UP)); //System.out.println(i+": "+sum); i++; } System.out.println(i); } }
3、x的x次幂结果为10 如果x的x次幂结果为10(参见【图1.png】),你能计算出x的近似值吗?
请把x的值计算到小数后6位(四舍五入),并填写这个小数值。
注意:只填写一个小数,不要写任何多余的符号或说明。
代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 package 校内选拔2015; public class T3 { public static void main(String[] args) { //System.out.println(Math.pow(2.5, 2.5)); double a=2.5; double c=0; while(Math.abs(c-10)>0.000001){ c=Math.pow(a, a); //System.out.println(c+" "+a); a=a+0.0000001; } System.out.println(a); } }
4、以74开头的 今有7对数字:两个1,两个2,两个3,…两个7,把它们排成一行。
17126425374635
当然,如果把它倒过来,也是符合要求的。
请你找出另一种符合要求的排列法,并且这个排列法是以74开头的。
注意:只填写这个14位的整数,不能填写任何多余的内容,比如说明注释等。
不写代码也能推断出来:
1 2 3 4 5 6 7 8 9 10 11 12 13 由题目要求可知要填的数为:74 _ _ _ _ 4 _ 7 _ _ _ _ _ 因为5和6之间分别要有5个、6个不同的数,所以5和6肯定都是在4 _ 7两边。 列出6可能的排列情况如下: 74 _ _ _ 64 _ 7 _ _ _ 6 _ 74 _ _ 6 _ 4 _ 7 _ _ 6 _ 74 _ 6 _ _ 4 _ 7 _ 6 _ _ 746 _ _ _ 4 _ 7 6 _ _ _ _ 列出5可能的排列情况如下: 74 _ _ _ 54 _ 7 _ 5 _ 74 _ _ 5 _ 4 _ 7 _ 5 _ _ _ 74 _ 5 _ _ 4 _ 7 5 _ _ _ _ 根据6和5的排列情况再对1,2,3进行排列,最后得出的结果是74151643752362
5、勾股定理 勾股定理,西方称为毕达哥拉斯定理,它所对应的三角形现在称为:直角三角形。
已知直角三角形的斜边是某个整数,并且要求另外两条边也必须是整数。
求满足这个条件的不同直角三角形的个数。
【数据格式】
例如,输入:
再例如,输入:
再例如,输入:
资源约定:
请严格按要求输出,不要画蛇添足地打印类似:“请您输入…” 的多余内容。
所有代码放在同一个源文件中,调试通过后,拷贝提交该源码。
代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 package 校内选拔2015; import java.util.Scanner; public class T5 { public static void main(String[] args) { Scanner sc=new Scanner(System.in); int n=sc.nextInt(); long nn=n*n; long a=0,c=0; long count=0; for (int i = 1; i < n; i++) { a=nn-i*i; c=(long)Math.pow(a, 0.5); if(c*c==a){ //System.out.println(n+" "+i+" "+c); count++; } } System.out.println(count/2); } }
8、标题:分机号 X老板脾气古怪,他们公司的电话分机号都是3位数,老板规定,所有号码必须是降序排列,且不能有重复的数位。比如:
751,520,321 都满足要求,而,
现在请你计算一下,按照这样的规定,一共有多少个可用的3位分机号码?
请直接提交该数字,不要填写任何多余的内容。
代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 package 校内选拔2015; public class T8 { public static void main(String[] args) { int count=0; for (int i = 0; i < 10; i++) { for (int j = i+1; j < 10; j++) { for (int h = j+1; h < 10; h++) { //System.out.println(i+""+j+h); count++; } } } System.out.println(count); } }
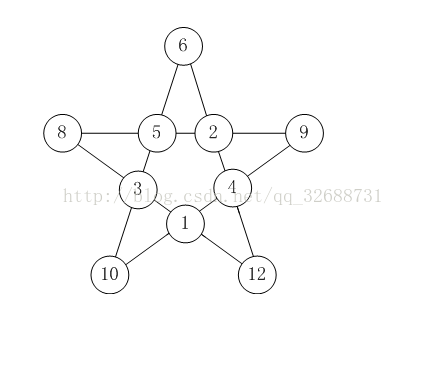
9、标题:五星填数 如【图1.png】的五星图案节点填上数字:1~12,除去7和11。
请你利用计算机搜索所有可能的填法有多少种。
请提交表示方案数目的整数,不要填写任何其它内容。
代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 package 校内选拔2015; public class T9 { static int count=0; public static void main(String[] args) { int[] data=new int[]{1,2,3,4,5,6,8,9,10,12}; f(data,0); System.out.println(count/10); } private static void f(int[] data, int k) { if(k==9){ if(check(data)){ count++; } } for (int i = k; i < data.length; i++) { {int t=data[k];data[k]=data[i];data[i]=t;}; f(data,k+1); {int t=data[k];data[k]=data[i];data[i]=t;}; } } private static boolean check(int[] data) { int n=data[0]+data[1]+data[2]+data[3]; if(n!=data[0]+data[4]+data[5]+data[6]) return false; if(n!=data[7]+data[1]+data[4]+data[8]) return false; if(n!=data[7]+data[2]+data[9]+data[6]) return false; if(n!=data[3]+data[9]+data[5]+data[8]) return false; return true; } }